コロナ
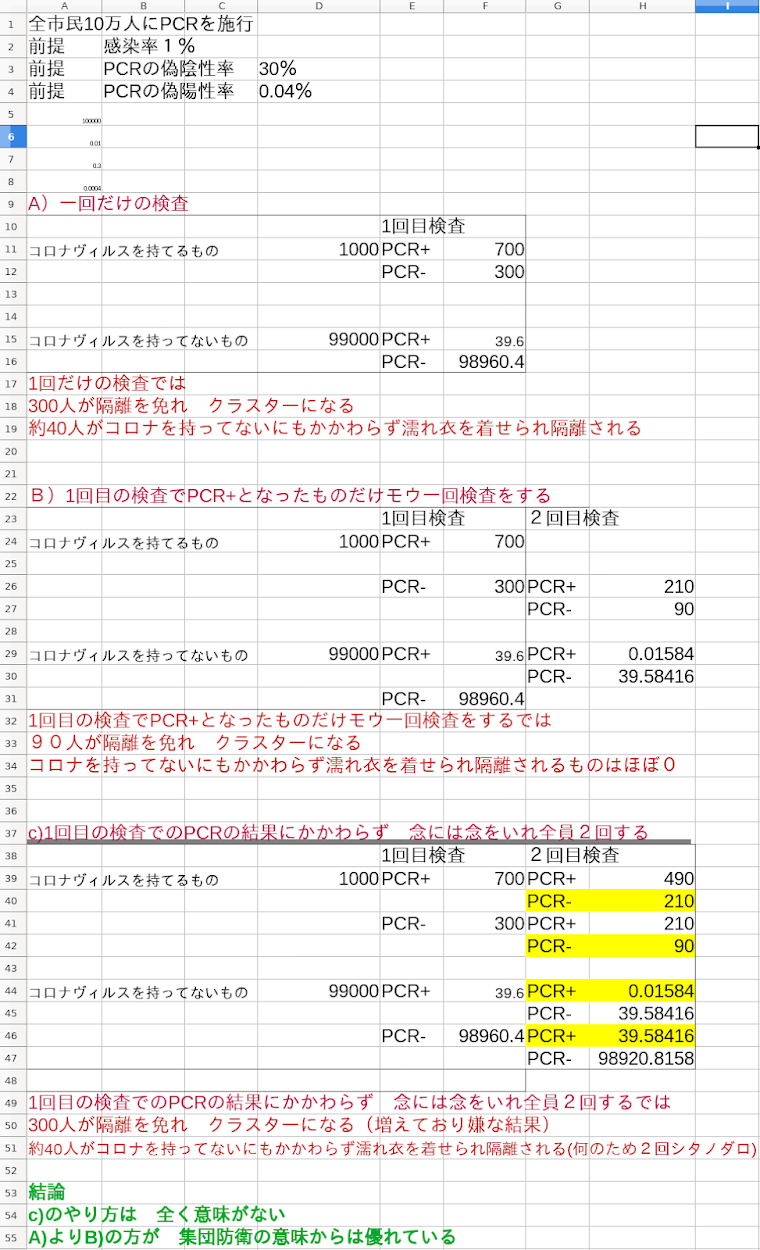
以下書きましたが 統計学不案内なのでどなたか検算お願いします コロナ検査の集団的防衛の意味合い コロナ検査の結果の解釈 こっちは ベイズの定理 を使わないといけない https://qiita.com/ea-yasuda/items/1ffcd518af18c6fa0063 にかかれている つまり 当たりくじを引いたとき その当たりくじは 赤からでたのか 青から出たのか その確率を計算することだ 「 一般的に、原因 → 結果となる確率は求めやすいけど、結果 → 原因となる確率は見出しづらいのですが、こういうときに使われる 」 これは https://bellcurve.jp/statistics/course/6448.html を直接つかうと 病気に罹患している確率：1％ 病気に罹患していない確率：99％ 実際に罹患している人が 検査で陽性となる確率：70％ 実際に罹患していない人が 検査で陰性となる確率：99.96％ 実際に罹患していない人が 検査で陽性となる確率：0.04％ なので PCRで 陽性と判定されたときに実際にコロナを持っている確率は ９４．６％ となります これでは まるで人まね子猿だ 自立しよう それには https://www.youtube.com/watch?v=oUN_GhB00fU&t=604s を参考にして PCRで陰性と判定されたが 実際にはコロナを持っている確率は なので の計算で 5.3％となる 結論 PCRで陽性と出たとき 本当にコロナに罹ってる確率は 94.6％ コロナに罹ってないのに罹っていると誤判断される率は 5.3％ と計算されます PCRで陰性とでたが 実際にはかかってる 確率は （社会防衛的には これが一番大事かも） 同様にして P(罹|陰)=P(陰|罹) * P(罹) / P(陰) =30*1/(1*30 + 99*99.96) =0.0030223533251931287 よって 0.3％となる それにしても ヨビノリさん クリアですねー さてこの結果をどう解釈するかは 数学の範囲外 以下の上の表は 非罹患者にはPCR陽性が0.04％しかでない場合で 罹患者割合を変えて シュミレーションしてみた 以下の下の表は 非罹患者にはPCR陽性が１％もでる場合で 罹患者割合を変えて